Today we learned about transforming functions,translating, reflecting, and stretching/compressing.
Here is an original problem:
y = f (x)
Translating Functions
Translation occurs when we move the graph units up/down or right/left
Moving a function up or down:
y = f (x) + c
where c is the number of units moved. If c is positive (as it is above), the function will move up c units; however, if c is negative, the function will move down c units.
If we were to translate the original problem down two units, the end formula would look like:
y = f (x) - 2
Moving a function left or right:
y = f (x - c)
C is still the number of units moved, however the graph is now moved to the left or to the right. If c is positive, the function will move c units to the left. If c is negative, the function will move c units to the right.
If we were to translate the original problem to the left 4 units, the end formula would look like:
y = f (x + 4)
A combination of movements left/right and up/down would look like this:
y = f (x - 3) + 2
where the original function will be translated 3 units to the right and up 2 units.
Stretching or compressing functions
Stretching/Compressing occurs when we move the graph c times away from the x or y axis.
Stretching a function:
y = c * f (x)
where c is the number of units moved. The graph will be pulled from the x-axis c times. The x-intercepts stay the same.
If we were to stretch the original problem by 2, the end formula would look like:
y = 2 f (x)
which would result in a 2x distance from the x-axis.
Compressing a function:
y = f (c * x)
C is still the number of units moved, however the graph is now compressed. If c is a large number (like 42), the function compresses more closely to the y-axis. If c is a small number (like 0.2), the function stretches from the y-axis.
If we were to compress the original problem by 4, the end formula would look like:
y = f (4x)
which would result in a 4x distance from the y-axis.
A combination of stretching from the x and y axis would look like this:
y = 3 f (0.1 x)
where the original function will be 3x away from the x-axis and 0.1x away from the y-axis [which would actually be closer because it is less than the original function (which was 1)].
Reflecting Functions
Reflecting occurs when we reflect the graph across the x or y axis.
Reflecting a graph across the x-axis looks like:
y = - f (x)
where the function's x-coordinates remain the same; however, all the y-coordinates become negative, and reflect across the x-axis.
Reflecting a graph across the y-axis:
y = f (-x)
where the function 's x-coordinates become negative; however, all the y-coordinates remain the same, and reflect across the y-axis.
Combination of the Functions
A combination of all three types of transforming functions would look like:
y = -3 f (x + 2) - 8
where the graph is:
- reflected across the x-axis
- stretched 3 units away from the x-axis
- translated 2 units to the left
- and translated 8 units down.











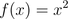






















.png)
.png)
.png)
.png)
.png)







.png)
.png)


.png)
.png)
.png)
.png)

